Разработка физической модели оптического датчика частоты вращения с математическим обоснованием

Число степеней свободы ν:

Где K – количество интервалов.

S – число параметров вероятностной математической модели (для экспоненциального распределения S=1, для других математических моделей S=2)

На основании таблицы можно сделать вывод что наши экспериментальные данные соответствуют вероятностной математической модели распределения - нормального закона распределения. Т. К. значения коэффициентов размаха вариации для данного закона находятся в заданных пределах. И не отвергается ни по одному критерию (Пирсона, Колмогорова, Романовского).

Кумулята интегральной функции распределения (теоретические значения).

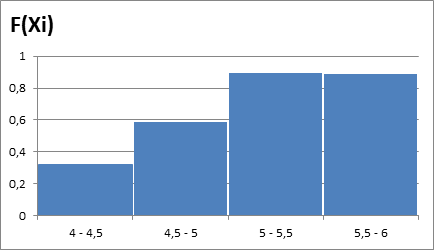
График интегральной функции распределения

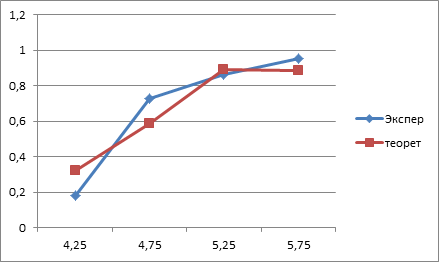
Анализ полученных результатов

В результате математической обработки результатов эксперимента было выявлено, что наиболее близко к экспериментальной характеристике, приближается нормальное распределение.

Для данного закона распределения дифференциальная функция имеет следующий вид:

Выражение для определения значений интегральной функции запишется следующим образом:

Произведена проверка адекватности вероятностной модели по трем критериям: по критерию Пирсона, по критерию согласия Колмогорова, и по критерию согласия Романовского.

Результаты проверки показали, что разработанная математическая модель согласуется с результатами эксперимента.

В данной работе был проведен анализ исследования оптического датчика зажигания. В результате была подобрана оптимальная математическая модель распределения, а также проведен анализ полученных результатов. Установлено, что рациональным математическим законом, описывающим математическую модель, является нормальный закон распределения.

Приложение 1

Давление воздуха