Разработка физической модели оптического датчика частоты вращения с математическим обоснованием

4) Определим среднее значение экспериментального распределения:

5) Определим дисперсию вариационного ряда:

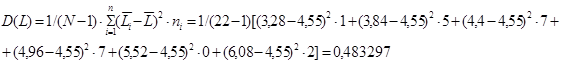
6) Среднее квадратичное отклонение:

7) Определим предельную абсолютную ошибку интервального оценивания математического ожидания:

, где:

α=0,05 - уровень значимости;

ν=N-1=21;

t0,05;21=2,2973.

8) Определяем доверительный интервал:

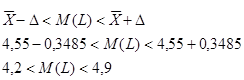
Таким образом, с вероятностью PD=1-0,05=0,95 математическое ожидание будет находиться в интервале от 4,2 до 4,9 и только 5% будет иметь математическое ожидание вне этого интервала.

8) Определим относительную точность оценки математического ожидания:

Это значит, что половина ширины доверительного интервала составляет 7,7% от величины среднего значения и характеризует относительную точность оценки математического ожидания.

9) Размах вариации экспериментальных результатов:

10) Размах колебаний выборки:

Из этого следует, что размах колебаний выборки вокрух среднего значения составляет 15%.

Подбор вероятностной математической модели

Для процессов ТЭА и решения практических задач наиболее характерны вероятностные математические модели, описывающие следующие законы распределения: нормальный, логарифмический нормальный, Вейбулла, экспоненциальный (показательный).

Нормальное распределение является двухпараметрическим. Параметр Х – оценка математического ожидания, характеризует положение центра рассеивания относительно начала отсчета, а параметр σх – среднее квадратичное отклонение характеризует растянутость распределения вдоль оси абсцисс. Физические закономерности формирования нормального распределения следующие. На протекание процесса и следовательно, формирование их показателей оказывает влияние сравнительно большое число независимых элементарных факторов, каждый из которых в отдельности оказывает ничтожное влияние на все вместе взятые. В этом случае процесс хорошо согласуется с мат моделью нормального распределения. Т. о, данное распределение весьма удобно для математического описания суммы случайных величин.

Логарифмически нормальное распределение имеет место тогда, когда не сама случайная величина, характеризующая результаты эксперимента, а ее логарифм распределен по нормальному закону. Физический смысл такое распределение формируется тогда, когда на протекание исследуемого процесса и его результат влияет сравнительно большое число случайных и независимых параметров, интенсивность действия которых зависит от достигнутого случайной величиной состояния. Эту модель удобно использовать для математического описания произведения исходных факторов.

Распределение Вейбулла – удобно если изучаемая система состоит из группы независимых элементов; отказ одного из них приводит к отказу всей системы.