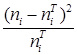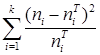Расчет и прогнозирование ресурса автомобиля

На основании полученных результатов (см. таблицу 4) строим графики дифференциальной и интегральной функций выбранного теоретического распределения. Для удобства построения по оси X – откладываем значения границ интервалов пробега до капитального ремонта в . По оси Y – значения .

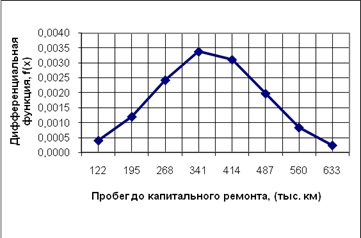
Рисунок 1.3 – График дифференциальной функции теоретического распределения

При построении графика интегральной функции распределения по оси Y откладываем значение F ().

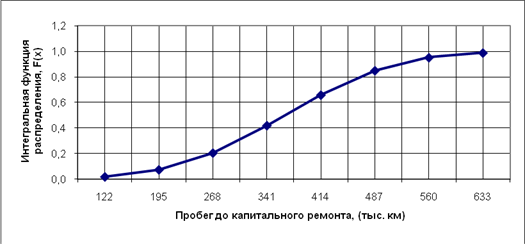
Рисунок 1.4 – График интегральной функции F () теоретического распределения

1.4 Проверка совпадения экспериментального и теоретического распределения

Для проверки совпадение экспериментального и теоретического распределения используем критерий Пирсона . Для расчета критерия Пирсона определяем теоретическую частоту попадания случайной величины в каждый из интервалов , т.е. количество автомобилей , потребовавших КР при пробеге в i-м интервале, определенное по теоретическому закону распределения:

(12)

где F(xi) – значение интегральной функции распределения для границы интервала хi, принимаются по таблице 4.

Расчетное значение критерия определяется по формуле:

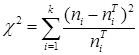.(13)

Результаты расчета представим в таблице 5.

Таблица 1.5 – Расчет критерия Пирсона