Прогнозирование грузооборота автотранспортного предприятия
Определяем коэффициенты регрессии ![]() и
и ![]() :
:
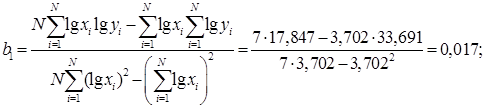 (3.4)
(3.4)
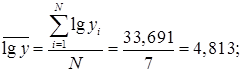 (3.5)
(3.5)
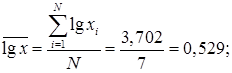 (3.6)
(3.6)
![]() . (3.7)
. (3.7)
Полученное уравнение регрессии имеет вид:
![]() (3.8)
(3.8)
где ![]() – рассчитанное по модели значение грузооборота, в тыс.
– рассчитанное по модели значение грузооборота, в тыс.
тонно-километров; х – условный год.
Проверка адекватности полученной регрессионной модели
Для оценки регрессионной модели используем критерий Фишера. Экспериментальное значение критерия Фишера:
![]()
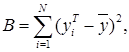
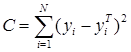 , (3.9)
, (3.9)
где ![]() ,
, ![]() – экспериментальное и теоретическое значение; d – число коэффициентов регрессии разработанной регрессионной модели: d = 2.
– экспериментальное и теоретическое значение; d – число коэффициентов регрессии разработанной регрессионной модели: d = 2.
Математическая модель считается адекватной результатам эксперимента и ее можно использовать для решения инженерных задач, если выполняется условие:
![]() (4.0)
(4.0)
где ![]() – критическое значение критерия Фишера для уровня значимости
– критическое значение критерия Фишера для уровня значимости ![]() и числа степеней свободы:
и числа степеней свободы: ![]() и
и ![]() . Для уровня значимости
. Для уровня значимости ![]() :
: ![]() ;
; ![]() . Тогда критическое значение критерия Фишера равно:
. Тогда критическое значение критерия Фишера равно: ![]() =4,950. Для определения экспериментального значения критерия Фишера составим таблицу 3.3.
=4,950. Для определения экспериментального значения критерия Фишера составим таблицу 3.3.
Таблица 3.3 – Данные для расчета критерия Фишера
|
№ п/п |
Год |
Условный год, хi |
Грузооборот |
Грузооборот |
|
| |||
|
1 |
2000 |
1 |
61126 |
63680,6 |
6525981,2 |
1846066 | |||
|
2 |
2001 |
2 |
63090 |
64435,4 |
1810152,2 |
364672 | |||
|
3 |
2002 |
3 |
64618 |
64881,1 |
69221,9 |
25027 | |||
|
4 |
2003 |
4 |
65542 |
65199,2 |
117522,2 |
25563 | |||
|
5 |
2004 |
5 |
66390 |
65447,0 |
889279,4 |
166206 | |||
|
6 |
2005 |
6 |
67072 |
65650,1 |
2021659,5 |
373137 | |||
|
7 |
2006 |
7 |
67437 |
65822,4 |
2606884,2 |
613269 | |||
|
Cумма |
455275 |
|
|
| |||||
Среднее значение ![]() определяется:
определяется:
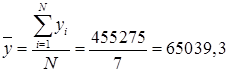 (тыс. тонно-километров). (3.10)
(тыс. тонно-километров). (3.10)
Экспериментальное значение критерия Фишера:
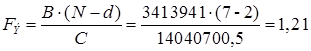 . (3.11)
. (3.11)
Математическая модель считается адекватной, т. к. выполняется условие:
![]() . (3.12)
. (3.12)
Прогнозирование грузооборота
Выполняем прогнозирование грузооборота на 3 года вперед и строим графики изменения грузооборота по статистическим данным и по разработанной математической модели (см. формулу 3.16). Для удобства построения результаты расчета сведем в таблицу 3.4.
Таблица 3.4 – Изменение грузооборота по годам
|
№ п/п |
Год |
Условный год, хi |
Грузооборот |
Грузооборот |
|
1 |
2000 |
1 |
61126 |
63680,6 |
|
2 |
2001 |
2 |
63090 |
64435,4 |
|
3 |
2002 |
3 |
64618 |
64881,1 |
|
4 |
2003 |
4 |
65542 |
65199,2 |
|
5 |
2004 |
5 |
66390 |
65447,0 |
|
6 |
2005 |
6 |
67072 |
65650,1 |
|
7 |
2006 |
7 |
67437 |
65822,4 |
|
8 |
2007 |
8 |
- |
65972,0 |
|
9 |
2008 |
9 |
- |
66104,2 |
|
10 |
2009 |
10 |
- |
66222,7 |
Значение гр
Разделы
- Главная
- Понятие и значение экономики транспорта
- Проектирование участка улицы
- Тепловозы на природном газе
- Особенности транспортной логистики
- Экспорт транспортных услуг
- Электрооборудование автомобилей
- Материалы
- Карта сайта
