Анализ влияния атмосферной турбулентности на продольное движение самолета БОИНГ-727
Цель работы – освоить и углубить теоретические знания и приобрести практические навыки анализа функционирования динамических систем, подверженных воздействию случайных возмущений. В качестве динамической системы рассматривается продольное движение в турбулентной атмосфере.
Уравнения движения самолета относительно инерциальной системы отсчета могут быть получены из основных теорем динамики твердого тела. Движение твердого тела описывается векторными уравнениями:
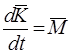
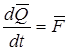
![]() и
и ![]() – главный вектор и главный момент
относительно центра масс количества движения твердого тела (
– главный вектор и главный момент
относительно центра масс количества движения твердого тела (![]() ,
, ![]() );
);
![]() и
и ![]() - главный вектор и главный момент относительно
центра масс внешних сил, действующих на твердое тело.
- главный вектор и главный момент относительно
центра масс внешних сил, действующих на твердое тело.
Если рассматривать самолет как твердое тело в произвольный момент времени и используя принцип “затвердевания”, то векторные уравнения количества движения и момента количества движения самолета в инерциальной системе отсчета примут вид:
![]()
![]() - уравнение описывающее
поступательное движение центра масс самолета (уравнение сил).
- уравнение описывающее
поступательное движение центра масс самолета (уравнение сил).
![]() - уравнение
описывающее вращательное или угловое движение вокруг центра масс самолета
(уравнение моментов).
- уравнение
описывающее вращательное или угловое движение вокруг центра масс самолета
(уравнение моментов).
Где ![]() и
и
![]() - количество движения и
момент количества движения относительно центра масс самолета как затвердевшей
системы переменного состава;
- количество движения и
момент количества движения относительно центра масс самолета как затвердевшей
системы переменного состава; ![]() и
и ![]() - главный вектор и главный момент внешних сил,
не связанных с работой двигательной установки;
- главный вектор и главный момент внешних сил,
не связанных с работой двигательной установки; ![]() и
и ![]() - тяга двигателей и момент тяги двигателей
относительно центра масс;
- тяга двигателей и момент тяги двигателей
относительно центра масс; ![]() и
и
![]() - главный вектор и
главный момент относительно центра масс кориолисовых сил инерции.
- главный вектор и
главный момент относительно центра масс кориолисовых сил инерции.
Пренебрегая скоростью и ускорением перемещения центра масс самолета относительно его корпуса, вычисляем производную согласно принципу затвердевания:
![]()
где m
– масса самолета; ![]() -
абсолютная скорость его центра масс.
-
абсолютная скорость его центра масс.
Пренебрегая влиянием кориолисовых и вариационных сил и моментов, связанных с движением масс топлива и газа внутри самолета, получаем:
![]()
![]()
Удобнее исследовать движение
самолета, пользуясь подвижными системами координат вначале с центром масс
самолета. При проектировании производной по времени от какого-либо вектора ![]() (определенного относительно
системы отсчета
(определенного относительно
системы отсчета ![]() ) на оси
любой подвижной системы координат OXYZ,
вращающейся с угловой скоростью
) на оси
любой подвижной системы координат OXYZ,
вращающейся с угловой скоростью ![]() относительно выбранной системы отсчета
(неподвижной):
относительно выбранной системы отсчета
(неподвижной):
|
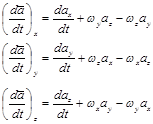
Где ![]() - проекции вектора
- проекции вектора ![]() на оси системы ОХYZ;
на оси системы ОХYZ;
![]() - их производные;
- их производные; ![]() - проекции угловой скорости
- проекции угловой скорости ![]() на оси системы OXYZ.
на оси системы OXYZ.
![]()
![]()
![]() Y
Y
![]()
![]()
![]()
![]()
![]()
![]()
Z X
![]()
![]()
![]()
![]()
Перепишем полученную систему для
вектора скорости ![]() :
:
![]()
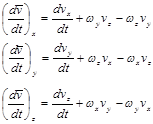
Для продольного движения самолета ![]() =
= ![]()
Принимая во внимание малость
абсолютных величин переносной и кориолисовой сил инерции, связанных с вращением
Земли: ![]()
![]()
где ![]() - вектор гравитационного ускорения;
- вектор гравитационного ускорения; ![]() - главный вектор
аэродинамических сил.
- главный вектор
аэродинамических сил.
Векторное уравнение движения центра масс самолета примет вид:
|
где ![]() - вектор скорости движения центра масс самолета
относительно Земли;
- вектор скорости движения центра масс самолета
относительно Земли; ![]() -
главный вектор аэродинамических сил;
-
главный вектор аэродинамических сил; ![]() - сила тяжести.
- сила тяжести.
Наиболее простую и удобную форму
система динамических уравнений движения центра масс самолета примет, если
векторное уравнение спроектировать на оси траекторной системы координат ![]() .
.
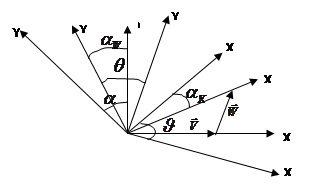
![]() -кинематический угол атаки
-кинематический угол атаки
![]() -угол атаки ветра
-угол атаки ветра
![]() - угол атаки
- угол атаки
![]()
|
|
![]() -угол тангажа
-угол тангажа
Применяя формулу (1) для проектирования
левой части уравнения (2) и учитывая, что ![]() , получим:
, получим:
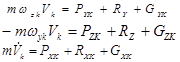 |
|||||
для продольного движения будет отсутствовать уравнение:
Проекции аэродинамической силы на оси траекторной системы координат выражаются через проекции на скоростные оси (для продольного движения):
![]()
![]()
![]()
где ![]() -сила лобового сопротивления;
-сила лобового сопротивления;![]() - подъемная сила.
- подъемная сила.
Используя матрицу направляющих косинусов между осями связанной и траекторной систем координат, проекции тяги двигателей на оси траекторной системы координат получим в следующем виде (для продольного движения):
![]() ;
; ![]()
Сила тяжести самолёта приложена в его центре масс, направлена по местной вертикали вниз и, следовательно, расположена в плоскости OXKYK траекторной системы координат. Её проекции на оси этой системы координат имеют вид (для продольного движения):
![]()
Тогда система динамических уравнений движения центра масс самолета в траекторной системе координат, примет вид:
![]()
![]()
![]()
Введем вектор воздушной скорости
самолёта ![]() , связанный с
векторами
, связанный с
векторами ![]() и
и ![]() (скорость ветра) соотношением:
(скорость ветра) соотношением:
![]()
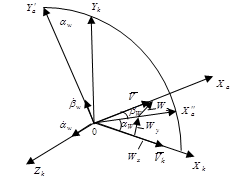
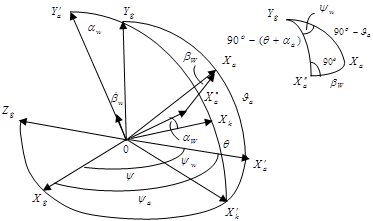
Отсюда получим соотношение, для проекций аэродинамических сил на оси траекторной системы координат с учетом ветра (для продольного движения):
![]()
![]()
В результате система динамических уравнений движения центра масс самолета получится в виде:
![]()
![]()
Исследования движения самолёта относительно центра масс удобно выполнять, если использовать динамические уравнения в проекциях на оси связанной системы координат. При изучении углового движения самолёта так же, как и при определении траекторий центра масс, применяют в качестве системы отсчёта неинерциальную систему, связанную с Землёй.
Проектируя векторное уравнение на оси связанной системы координат и применяя формулы (1) для вычисления проекций производных по времени от вектора кинетического момента самолёта, получим систему скалярных уравнений движения самолёта относительно центра масс:
![]()
![]() ;
;
![]() ;
;
![]() .
.
![]() - проекции вектора кинетического момента
самолета на связанные оси координат,
- проекции вектора кинетического момента
самолета на связанные оси координат,
![]() - проекции вектора абсолютной угловой скорости
самолета на те же оси,
- проекции вектора абсолютной угловой скорости
самолета на те же оси,
![]() - проекции главного момента аэродинамических сил
и сил тяги относительно центра масс на те же оси.
- проекции главного момента аэродинамических сил
и сил тяги относительно центра масс на те же оси.
![]()
![]()
![]()
![]()
Поскольку основная плоскость ОХУ
связанной системы координат является плоскостью симметрии самолета, то ![]() =
=![]() = 0.
= 0.
Тогда система уравнений примет вид:
![]()
![]()
![]()
![]()
Для продольного движения самолета ![]() то:
то:
![]()
Кинематические уравнения связывают между собой кинематические и геометрические характеристики поступательного движения центра масс самолёта и вращения его относительно центра масс, а также угловые скорости подвижных систем координат с параметрами движения самолёта.
Кинематическое уравнение движения центра масс самолета в векторной форме
![]()
где ![]() - радиус-вектор и вектор скорости центра масс
самолета относительно рассматриваемой системы отсчета. Для получения скалярных
кинематических уравнений движения центра масс найдем проекции вектора скорости центра
масс самолета на оси координат, относительно которых рассматривается движение
самолета. Проектируя вектор скорости
- радиус-вектор и вектор скорости центра масс
самолета относительно рассматриваемой системы отсчета. Для получения скалярных
кинематических уравнений движения центра масс найдем проекции вектора скорости центра
масс самолета на оси координат, относительно которых рассматривается движение
самолета. Проектируя вектор скорости ![]() на нормальные оси координат и используя таблицу
направляющих косинусов, получим кинематические уравнения движения центра масс
самолета:
на нормальные оси координат и используя таблицу
направляющих косинусов, получим кинематические уравнения движения центра масс
самолета:
![]()
![]() - координата самолета в стартовых осях.
- координата самолета в стартовых осях.
Кинематические уравнения,
описывающие вращение самолета относительно нормальной системы координат,
устанавливают связь между производными углов ![]() -по времени и проекциями на связанные оси
вектора угловой скорости
-по времени и проекциями на связанные оси
вектора угловой скорости ![]() самолета
относительно системы отсчета, связанной с Землей. Поскольку вращение самолета
может быть представлено как изменение углов
самолета
относительно системы отсчета, связанной с Землей. Поскольку вращение самолета
может быть представлено как изменение углов ![]() , определяющих положение самолета относительно
Земли, вектор угловой скорости самолета
, определяющих положение самолета относительно
Земли, вектор угловой скорости самолета ![]() равен геометрической сумме угловых скоростей
элементарных поворотов
равен геометрической сумме угловых скоростей
элементарных поворотов
![]() .
.
Это уравнение является
кинематическим уравнением вращательного движения самолета в векторной форме.
Проектируя векторы ![]() на
направление связанных осей OX,
OY и OZ
получим:
на
направление связанных осей OX,
OY и OZ
получим:
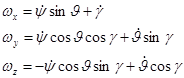
Для продольного движения получим:
![]()
В результате получим систему уравнений продольного движения самолёта с учётом ветра:
![]()
![]()
![]()
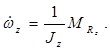 (*)
(*)
![]()
![]()
- Линеаризация дифференциальных уравнений движения самолёта
- Вывод передаточных функций
- Характеристики турбулентной атмосферы. Описание метода вычисления дисперсии
Разделы
- Главная
- Понятие и значение экономики транспорта
- Проектирование участка улицы
- Тепловозы на природном газе
- Особенности транспортной логистики
- Экспорт транспортных услуг
- Электрооборудование автомобилей
- Материалы
- Карта сайта
