Линеаризация дифференциальных уравнений движения самолёта

Линеаризация функции в окрестности значения аргументов – разложение функции в ряд Тейлора по первым членам в этой окрестности:

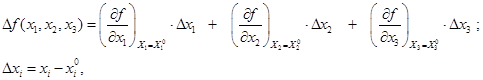
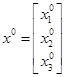- опорные значения аргументов.

При линеаризации д.у. переходят от самих параметров движения к их приращениям относительно опорных значений.

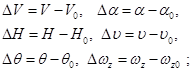
Соответственно производные: .

Опорным движением является установившийся горизонтальный полёт, поэтому:

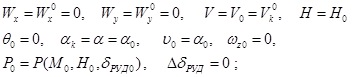
Линеаризация правых частей уравнений в системе (*):

1) в первом уравнении

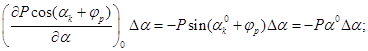
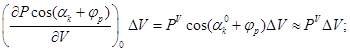
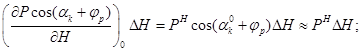
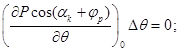
2) во втором уравнении

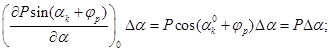
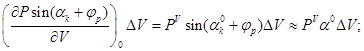
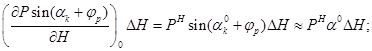
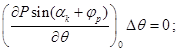
3) в третьем уравнении

Учитывая, что ,

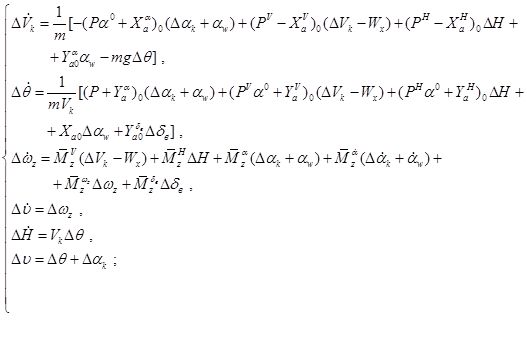
Выполнено следующее приближенное равенство:

так как:

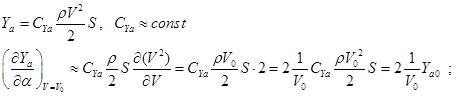
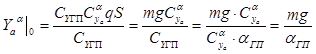
Так как самолёт дозвуковой имеем:

Следующие слагаемые являются малыми и ими можно пренебречь:

Также можно пренебречь тягой по сравнению с , по сравнению с .

Получаем:

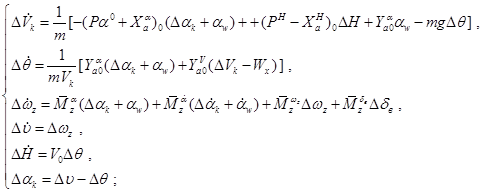
Пренебрежение слагаемыми позволяет исключить из рассмотрения уравнение для , положив .

Обозначим: , уравнения перепишутся в виде: