Уравнение движения рыскания

Допустим, что ЛА совершает горизонтальный полет с постоянной скоростью и управляется автопилотом. Для получения уравнений движения рыскания приравняем проекции внешних и инерционных сил на нормаль (ось Oz) к траектории, а также внешний и инерционный моменты относительно нормальной оси ЛА (оси Oyc):

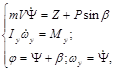
где Z – боковая аэродинамическая сила;

Y - угол поворота траектории;

Iy – момент инерции ЛА относительно связанной оси Oyc;

wy – скорость рыскания (угловая скорость ЛА относительно оси Oyc);

My – аэродинамический момент рыскания.

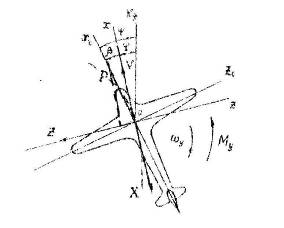
Рис.1. Схема сил и моментов действующих на объект

Линейные дифференциальные уравнения движения рыскания имеют вид:

,

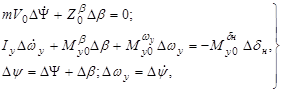где для постоянных коэффициентов введены следующие обозначения:

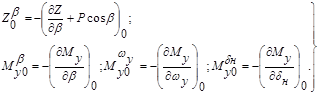
Нулевой индекс у скобок обозначает, что производная и параметры взяты для выбранного невозмущенного движения.

В некоторых случаях уравнения движения рыскания еще более упрощают. Дальнейшее упрощение этих уравнений основывается на том, что в большинстве режимов полета руль направления устраняет скольжение и можно положить, что Db=0. Тогда движение рыскания будет описываться одним уравнением:

Это же уравнение описывает движение ЛА, нейтрального в путевом отношении, т.е. ЛА, у которого коэффициент момента путевой устойчивости равен нулю: .

Если пренебречь движением центра масс под действием боковых сил и рассматривать лишь колебания продольной оси ЛА относительно вектора скорости, т.е. положить Db=Dy, то уравнение движения примет вид: