Принципы логистики в сфере транспорта

Цель работы: – найти кратчайшие расстояния между пунктами транспортной сети и заполнить ими соответствующую таблицу;

– найти кратчайшие пути проезда между пунктами и отразить их на соответствующем рисунке.

Исходными данными для выполнения данной практической работы является транспортная сеть из индивидуального задания (рис. Б1).

Живые елки с доставкой спб купить живые елки в спб с доставкой Диво Сад.

Для выполнения практической работы можно воспользоваться любым из известных методов, например, методом потенциалов [8]. Сущность его состоит в следующем. Потенциал одной из вершин (назовем ее исходной, например, вершины А) принимают за 0, то есть РА=0. Далее по формуле 1.1 определяются потенциалы всех вершин, непосредственно связанных с ней:

Рj = Рi + ℓij, (1.1)

где i, j – текущие индексы соответственно исходной и непосредственно связанной с ней вершин;

Рi – потенциал исходной вершины, км;

Рj – потенциал вершины, непосредственно связанной с исходной, км;

ℓij – длина звена между исходной и непосредственно связанной с ней

вершинами, км.

Из всех рассчитанных таким образом потенциалов выбирается наименьший, его значение записывается в таблицу кратчайших расстояний, а соответствующее звено на рисунке отмечается стрелкой. Далее вершина с наименьшим потенциалом принимается за исходную, от нее вновь определяются потенциалы всех вершин, непосредственно связанных с ней. Просматриваются все известные к этому моменту потенциалы (определенные как на предыдущем, так и на данном этапе), из них вновь выбирается наименьший, его значение заносится в эту же таблицу, а соответствующее звено на рисунке отмечается стрелкой. Таким образом, расчеты повторяются до полного заполнения таблицы и рисунка.

Рассмотрим метод потенциалов на примере рис. Б1.

Примем РА = 0.

С вершиной А непосредственно связаны вершины М, Б и В. Их

потенциалы:

РМ = РА+ℓАМ = 0+7 = 7 км;

РБ = РА+ℓАБ = 0+9 = 9 км;

РВ = РА+ℓАВ = 0+6 = 6 км.

Отсюда в строке А и столбце В табл. 1.1 проставляем минимальное расстояние 6, а звено АВ на рис. 1.1 отмечаем стрелкой. Вершину В принимаем за исходную.

Непосредственно с ней связаны вершины Б, Г и Д. Их потенциалы:

РВ = 6

РБ = 6 + 3 = 9 км.

РГ = 6 + 6 = 12 км

РД = 6 + 8 = 14 км

РЕ = 6 + 10 = 16 км

Из известных к этому моменту потенциалов (РМ = 7, РБ=9, РГ=12, РД=14, РЕ=16) выбираем наименьший (РМ = 7), число 7 заносим в табл. 1.1 в строку А и столбец М, звено АМ на рис. 1.1 отмечаем стрелкой. Вершину М принимаем за исходную, с ней непосредственно связаны вершины Н, Л и Б. Их потенциалы:

РМ = 7

РН = 7 + 8=15;

РЛ = 7 + 12=19;

РБ = 7 + 10 = 17.

Из известных к данному моменту потенциалов (РБ =9, РГ=12, РД=14; РЕ=16, РН=15, РЛ=19.) выбираем минимальный РБ=9, в строку А и столбец Б проставляем 9, звено АБ отмечаем стрелкой. Вершину Б принимаем за исходную, с ней непосредственно связана вершина Г (вершины М и В не берем в расчет, поскольку до них кратчайшее расстояния уже известны).

РБ =9

РГ = 9 + 6 = 15.

Минимальный потенциал имеет вершина Г (РГ = 12), ее значение заносим в табл. 1.1. в строку А и столбец Г, звено ВГ отмечаем стрелкой на рис. 1.1.

Таким образом, выбирая на каждом этапе минимальный потенциал, можно с абсолютной уверенностью гарантировать определение кратчайших расстояний и путей проезда от вершины А до всех остальных вершин данной транспортной сети. Расчеты повторяются до тех пор, пока все клетки в строке А табл. 1 не будут заполнены расстояниями. При этом на рис. 1 у каждой вершины должна быть обозначена хотя бы одна стрелка (кроме вершины А, поскольку это исходная вершина с потенциалом РА=0).

Таблица 1 Матрица кратчайших расстояний между пунктами транспортной сети

	А	Б	В	Г	Д	Е	Ж	З	И	К	Л	М	Н
А		9	6	12	14	16	18	21	25	26	19	7	15
Б	9		3	9	11	13	15	18	22	22	18	10	18
В	6	3		6	8	10	15	15	19	19	15	13	21
Г	12	9	6		3	8	6	9	13	13	9	19	15
Д	14	11	8	3		5	9	12	16	16	12	21	18
Е	16	13	10	8	5		5	8	12	12	17	23	23
Ж	18	15	15	6	9	5		3	7	7	14	25	20
З	21	18	15	9	12	8	3		10	4	11	23	17
И	25	22	19	13	16	12	7	10		8	15	27	21
К	26	22	19	13	16	12	7	4	8		7	19	13
Л	19	18	15	9	12	17	14	11	15	7		12	6
М	7	10	13	19	21	23	25	23	27	19	12		8
Н	15	18	21	15	18	23	20	17	21	13	6	8

Далее потенциал следующей вершины (например, Б) принимается за 0 и все расчеты повторяются аналогично.

Следует обратить внимание на то, что на данной транспортной сети нет никаких ограничений по организации дорожного движения, то есть расстояние, скажем, между пунктами А и И равно расстоянию между пунктами И и А (ℓАИ=ℓИА). Таким образом, матрица кратчайших расстояний (см. табл. 1.1) будет симметрична относительно диагонали, и можно заполнять только одну ее часть.

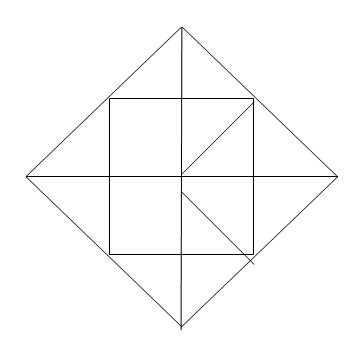Рисунок 1 – Кратчайшие пути проезда от вершины А

Вывод: в результате выполненной работы мы определили кратчайшие расстояния между пунктами транспортной сети.

• Закрепление потребителей однородного груза за поставщиками
• Маршрутизация перевозок грузов при помашинных отправках